Моделирование футбольного мяча в 3ds Max 2020

Покрышка классического футбольного мяча сшивается (или склеивается) из 32 отдельных панелей и имеет форму усеченного икосаэдра — полуправильного многогранника, состоящего из 20 правильных шестиугольников и 12 правильных пятиугольников. Форму сферы мяч приобретает за счет давления закачанного внутрь него воздуха. Что касается размера футбольного мяча, то во всех официальных соревнованиях, проводимых под эгидой ФИФА, используются мячи с длиной окружности от 68 до 70 см, что соответствует радиусу от 10,82 до 11,14 см. Процедура создания 3d-модели именно такого, шаблонного, футбольного мяча в программе 3ds Max описана в данном уроке…

Весь процесс моделирования футбольного мяча в 3ds Max можно условно разбить на следующие этапы:

• Настройка единиц измерения;
• Построение усеченного икосаэдра;
• Проработка топологии;
• Придание объекту сферической формы;
• Создание швов между панелями;
• Сглаживание модели;
• Корректировка размера футбольного мяча.

Далее подробно о каждом этапе моделирования…

Настройка единиц измерения

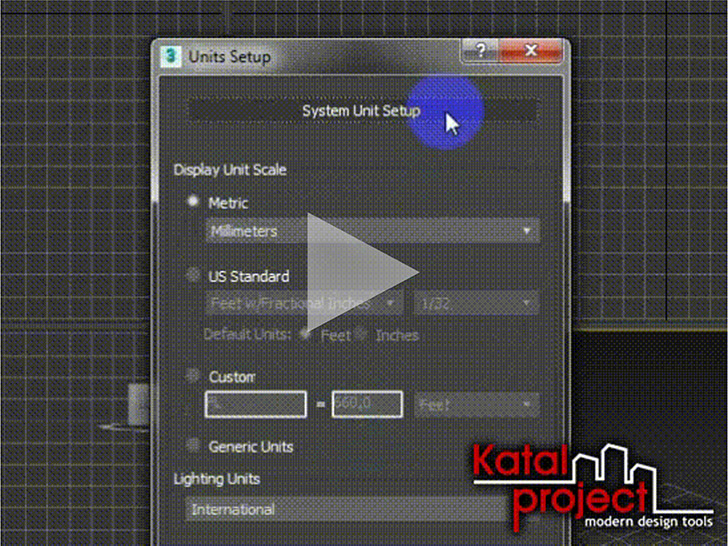
Прежде, чем приступать к моделированию, следует правильно настроить единицы измерения для сцены. Для создания модели футбольного мяча лучше всего подойдут миллиметры:

1. В диалоговом окне «Units Setup» (Настройка единиц измерения), в разделе «Display Unit Scale» (Отображаемые единицы измерения) отмечаем вариант Metric (Метрические), из соответствующего выпадающего списка выбираем Millimeters (Миллиметры);
2. В диалоговом окне «System Unit Setup» (Настройка системной единицы измерения) задаем: 1 Unit = 1,0 Millimeters.

Построение усеченного икосаэдра

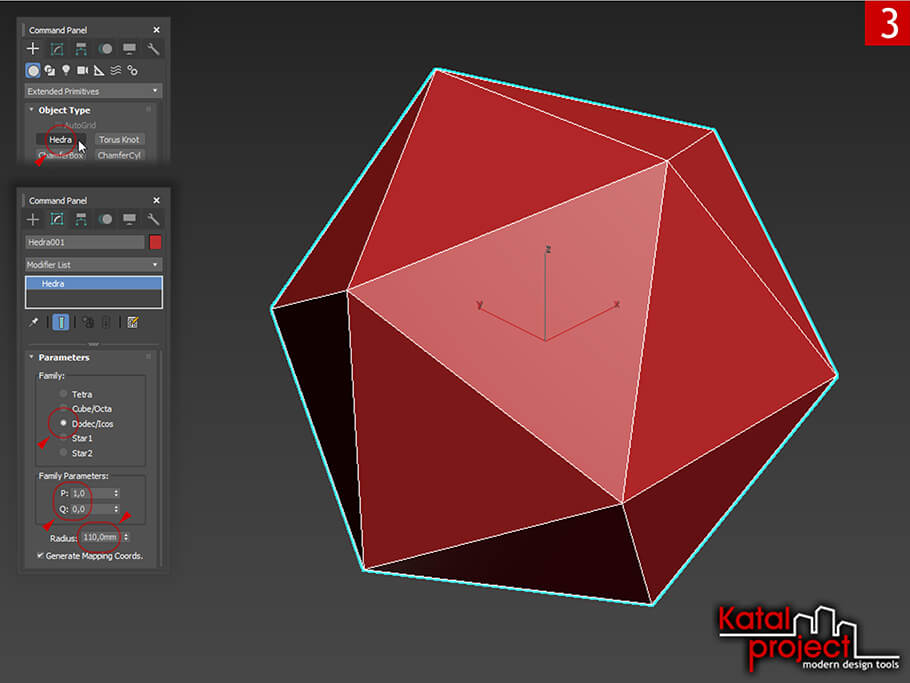
Сделать усеченный икосаэдр в 3ds Max проще всего из примитива «Hedra» (Многогранник), который можно найти среди «Extended Primitives» (Расширенных примитивов):

3. Добавляем на сцену «Hedra» (Многогранник) со следующими параметрами:
   • «Family» (Семейство) — Dodec/Icos (Додекаэдр/Икосаэдр);
   • «Family Parameters» (Параметры семейства): «P» — 1,0; «Q» — 0,0;
   • «Radius» (Радиус) — 110,0mm;
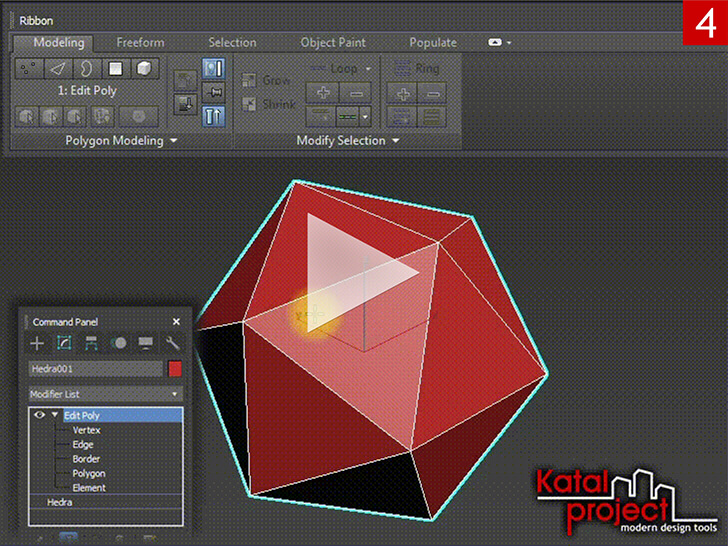
4. Усекаем полученный правильный икосаэдр:
   • Применяем к нему модификатор «Edit Poly» (Редактировать как многоугольник), активируем уровень «Edge» (Ребро) и выделяем все ребра объекта;
   • На панели «Edges» (Ребра) в поле «Number of Vertices» (Количество вершин) вводим 2 и выполняем команду «Insert Vertices» (Добавить вершины);
   • Все новые вершины объединяем между собой с помощью команды «Connect» (Соединить);
   • Выделяем все вершины, которые являются вершинами исходного правильного икосаэдра, и избавляемся от них с помощью команды «Remove» (Устранить);
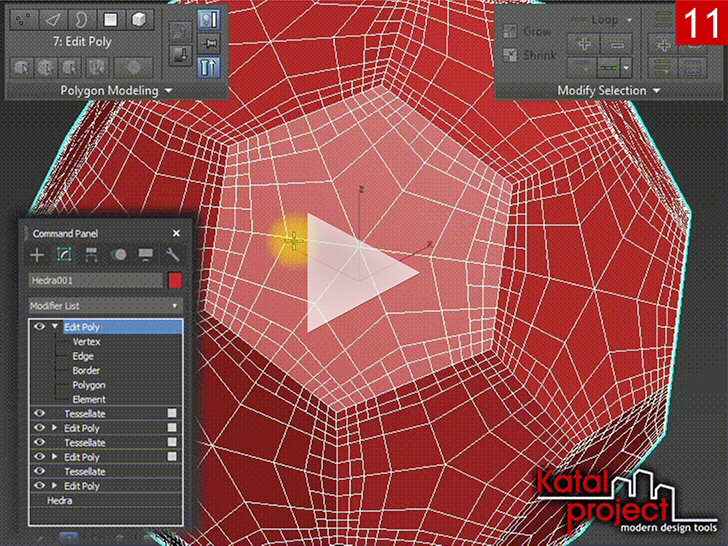
   • Переключаемся на уровень «Edge» (Ребро), выделяем ребра, которые образовались внутри шестиугольных граней усеченного икосаэдра, и избавляемся от них с помощью команды «Remove» (Устранить);
   • Выходим из режима работы с подчиненными объектами редактируемого многоугольника.

Проработка топологии

В процессе проработки топологии следует учитывать, что панели футбольных мячей обычно имеют достаточно резкие изгибы по краям, в непосредственной близости от швов между ними. Чтобы на модели эти изгибы получились достаточно плавными, гладкими, полигоны по краям панелей должны быть достаточно мелкими. А вот ближе к центру панелей, где искривления поверхности незначительны, вполне можно обойтись более крупными полигонами. Дробить полигоны будем в несколько этапов…

Этап 1

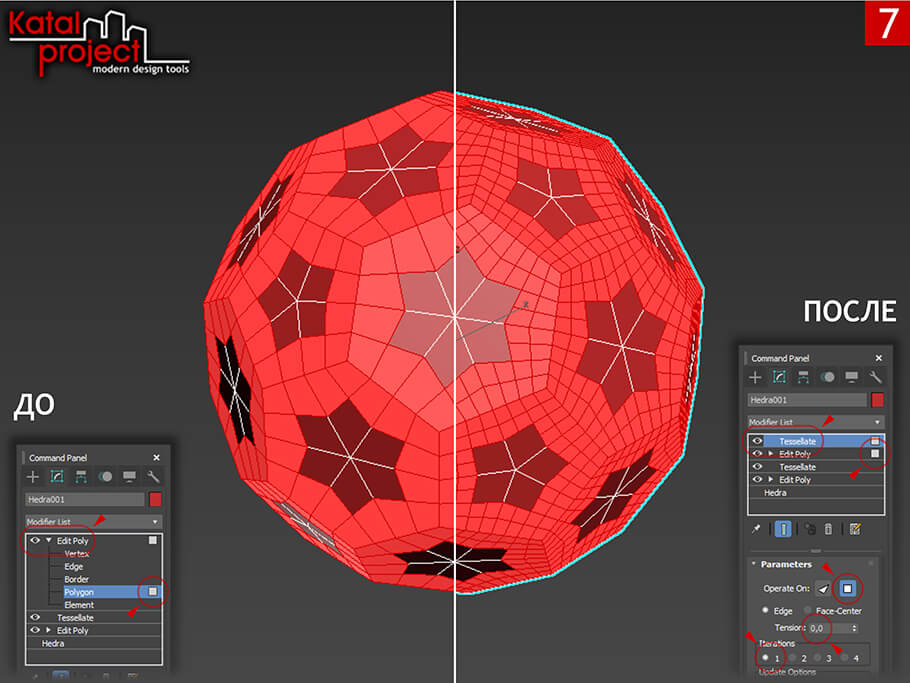
5. К полученному усеченному икосаэдру применяем модификатор «Tessellate» (Замостить), который настраиваем следующим образом:
   • «Operate On» (Действовать на) — Polygons (Полигоны), Edge (Ребро);
   • «Tension» (Натяжение) — 0,0;
   • «Iterations» (Повторения) — 2.

Этап 2

6. Выбираем полигоны, которые необходимо разбить на более мелкие:
   • В стек модификаторов добавляем модификатор «Edit Poly» (Редактировать как многоугольник), активируем уровень «Polygon» (Полигон) и выделяем все полигоны, примыкающие к ребрам многогранника;
7. Не снимая выделения берем из списка модификаторов «Tessellate» (Замостить), который настраиваем следующим образом:
   • «Operate On» (Действовать на) — Polygons (Полигоны), Edge (Ребро);
   • «Tension» (Натяжение) — 0,0;
   • «Iterations» (Повторения) — 1.
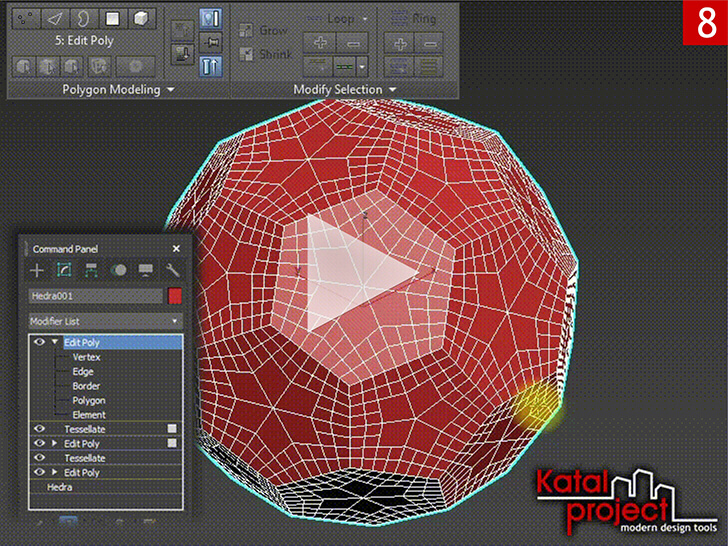
8. Удаляем лишние ребра:
   • В стек модификаторов добавляем еще один модификатор «Edit Poly» (Редактировать как многоугольник), активируем уровень «Edge» (Ребро) и выделяем все «тупиковые» цепочки ребер, обрывающиеся не доходя до центров панелей футбольного мяча;
   • Удаляем выделенные ребра с помощью команды «Clean Remove» (Устранить полностью).

Этап 3

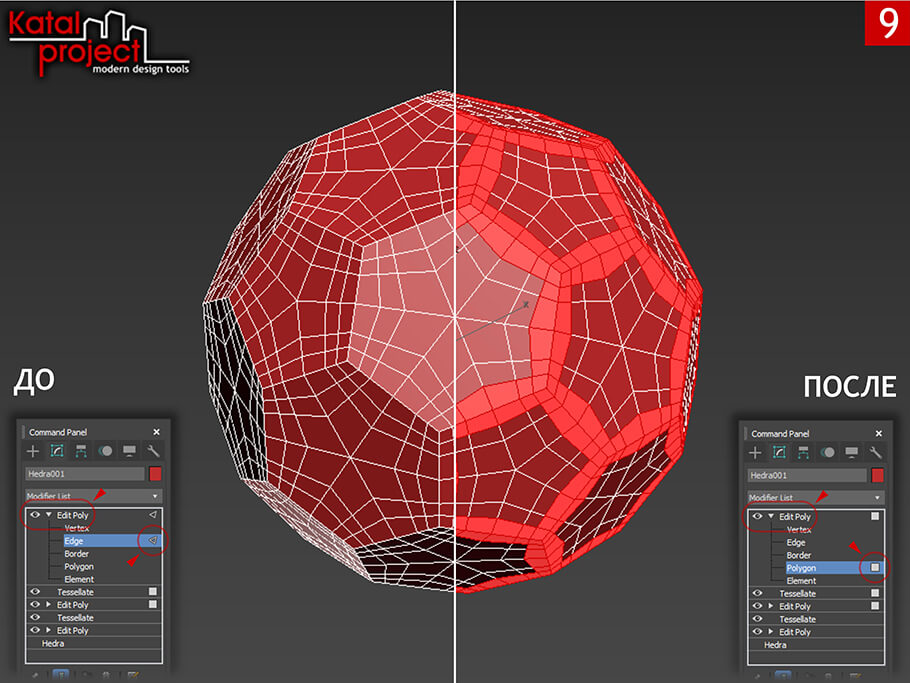
9. Выбираем следующую порцию полигонов, которые необходимо разбить на более мелкие:
   • Продолжая работать с тем же модификатором «Edit Poly» (Редактировать как многоугольник), переключаемся на уровень «Polygon» (Полигон) и выделяем все полигоны, примыкающие к ребрам многогранника;
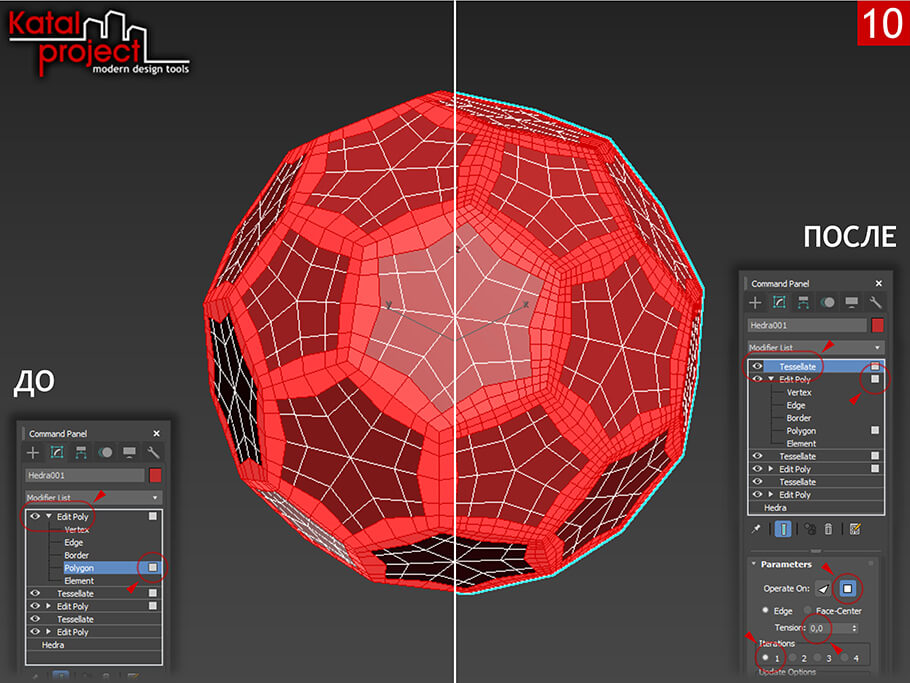
10. Не снимая выделения берем из списка модификаторов «Tessellate» (Замостить), который настраиваем следующим образом:
    • «Operate On» (Действовать на) — Polygons (Полигоны), Edge (Ребро);
    • «Tension» (Натяжение) — 0,0;
    • «Iterations» (Повторения) — 1;
11. Удаляем лишние ребра:
    • В стек модификаторов добавляем еще один модификатор «Edit Poly» (Редактировать как многоугольник), активируем уровень «Edge» (Ребро) и выделяем все «тупиковые» цепочки ребер, обрывающиеся не доходя до центров панелей футбольного мяча;
    • Удаляем выделенные ребра с помощью команды «Clean Remove» (Устранить полностью);
    • Выходим из режима работы с подчиненными объектами редактируемого многоугольника.

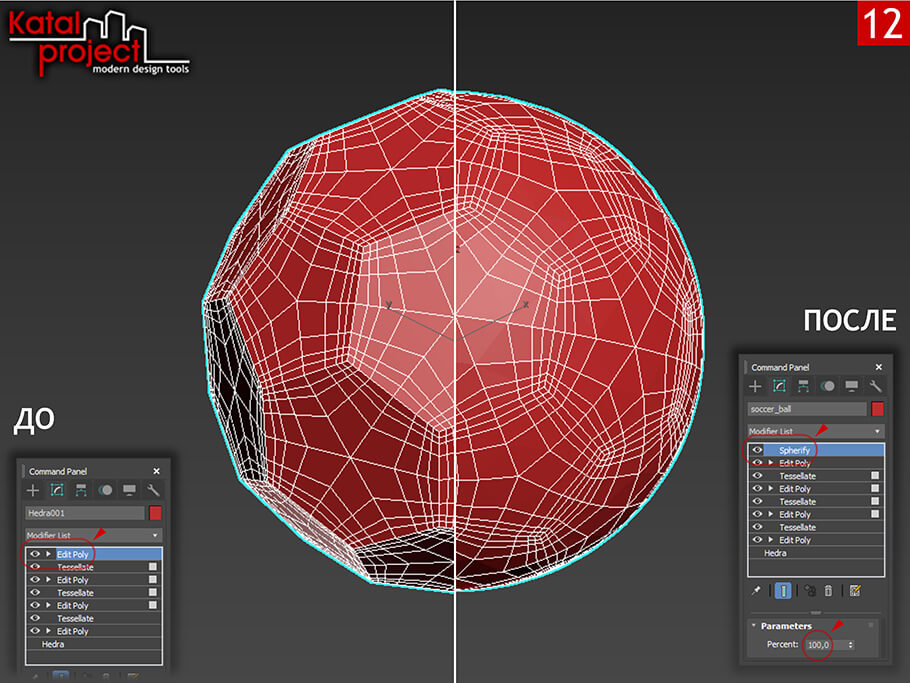
Придание объекту сферической формы

Чтобы «накачать» мяч, то есть придать смоделированному объекту сферическую форму:

12. Накидываем на него модификатор «Spherify» (Придать сферическую форму), параметр «Percent» (Процент) — 100,0.

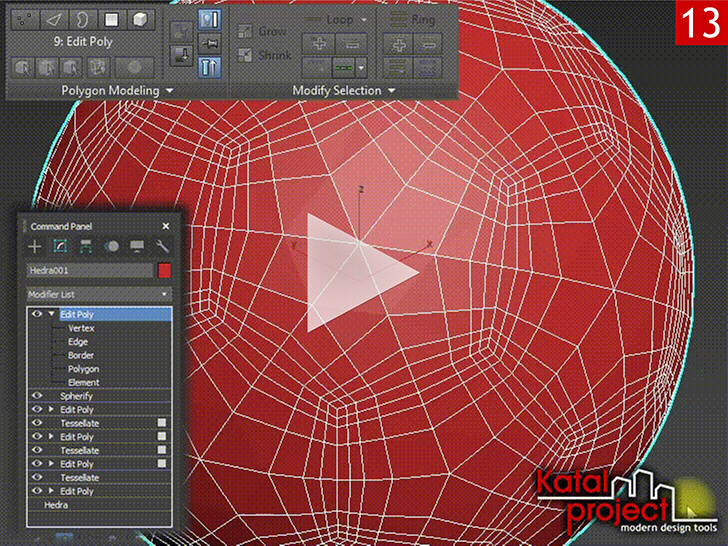
Создание швов

Чтобы на модели футбольного мяча появились швы, достаточно немного утопить в тело мяча ребра редактируемого многоугольника, которые принадлежат сторонам панелей мяча. А можно, наоборот, немного приподнять над поверхностью сферы полигоны панелей:

13. Делаем каждую панель мяча самостоятельным элементом редактируемого многоугольника:
    • Очередной раз берем модификатор «Edit Poly» (Редактировать как многогранник), активируем уровень «Edge» (Ребро) и выделяем все ребра на сторонах панелей;
    • Расщепляем выделенные ребра с помощью команды «Split» (Разделить);
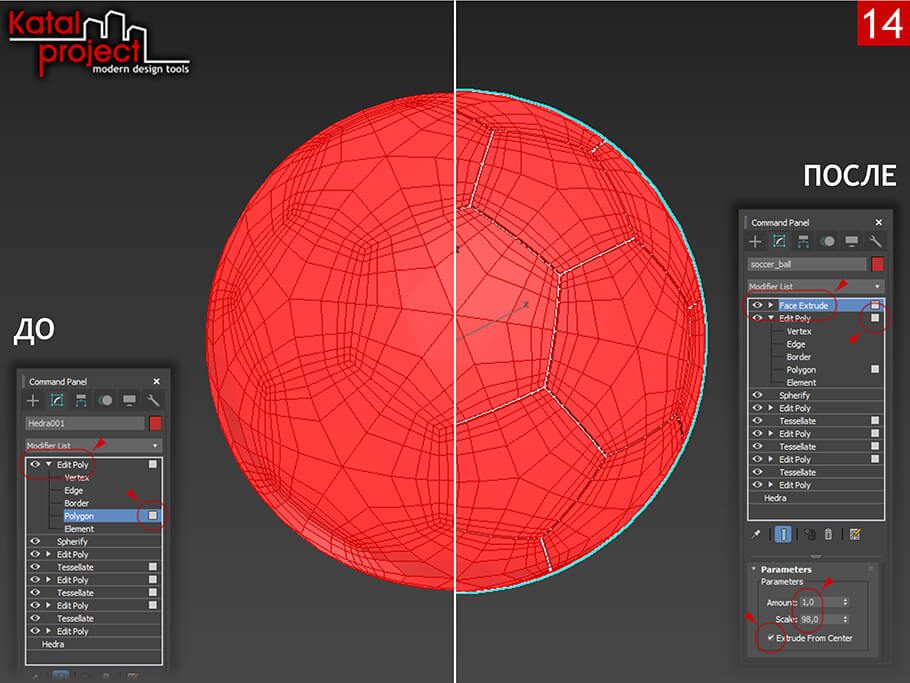
    • Переключаемся на уровень «Polygon» (Полигон) и выделяем все полигоны модели;
14. Не снимая выделения берем из списка модификаторов «Face Extrude» (Выдавить грани) со следующими параметрами:
    • «Amount» (Величина) — 1,0;
    • «Scale» (Масштаб) — 98,0;
    • Галочка «Extrude From Center» (Выдавливать из центра) — включена.

Сглаживание

Чтобы на модели мяча не было заметно ребер между гранями, модель необходимо сгладить, с чем прекрасно справится модификатор «TurboSmooth» (Турбо-сглаживание). Но чтобы модификатор отработал корректно, прежде чем применять его, объект необходимо к сглаживанию подготовить:

15. Объединить все элементы в один:
    • Поверх модификатора «Face Extrude» (Выдавить грани) накидываем модификатор «Edit Poly» (Редактировать как многогранник);
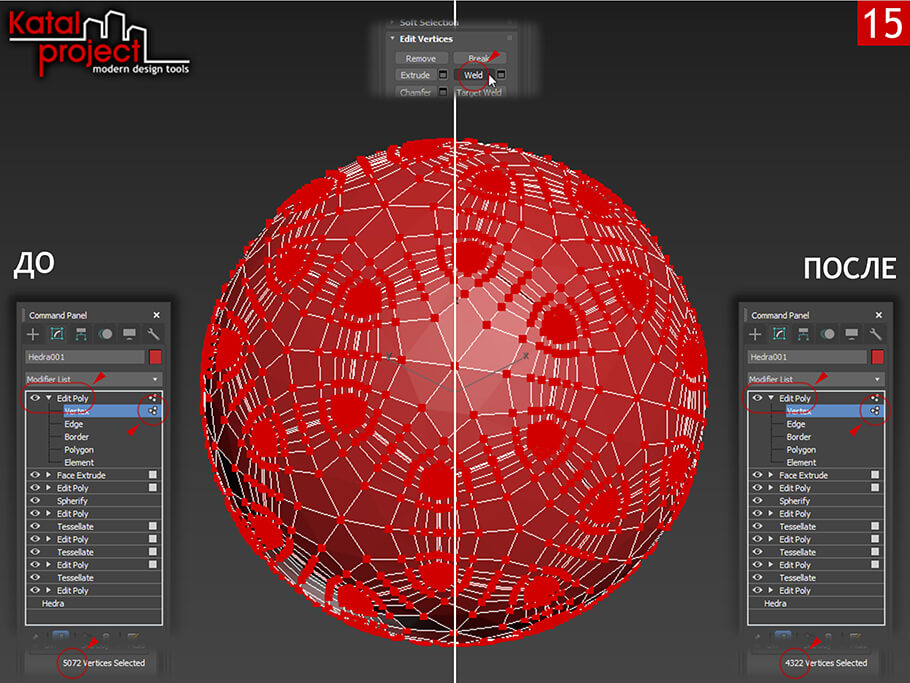
    • Активируем уровень «Vertex» (Вершина) и выделяем все вершины объекта;
    • Сливаем все совпадающие вершины с помощью команды «Weld» (Объединить);
16. Назначить полигонам подходящие группы сглаживания:
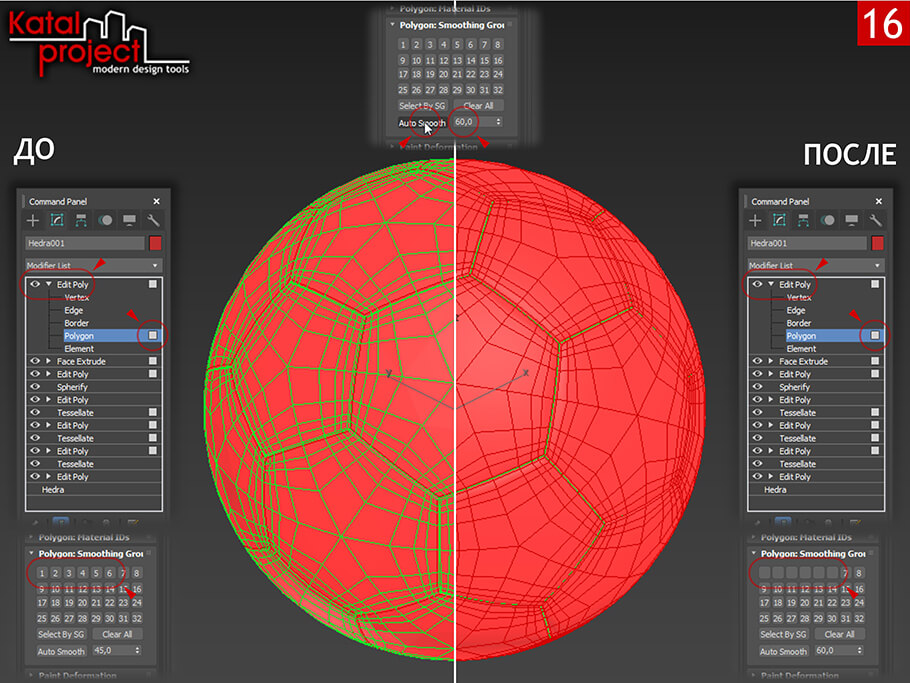
    • Продолжая работать с модификатором «Edit Poly» (Редактировать многогранник) переключаемся на уровень «Polygon» (Полигон) и выделяем все полигоны объекта;
    • В свитке «Polygon: Smoothing Groups» (Полигон: группы сглаживания) в поле «Threshold» (Порог) вводим 60,0 и выполняем команду «Auto Smooth» (Сгладить автоматически);
    • Выходим из режима работы с подчиненными объектами редактируемого многогранника.

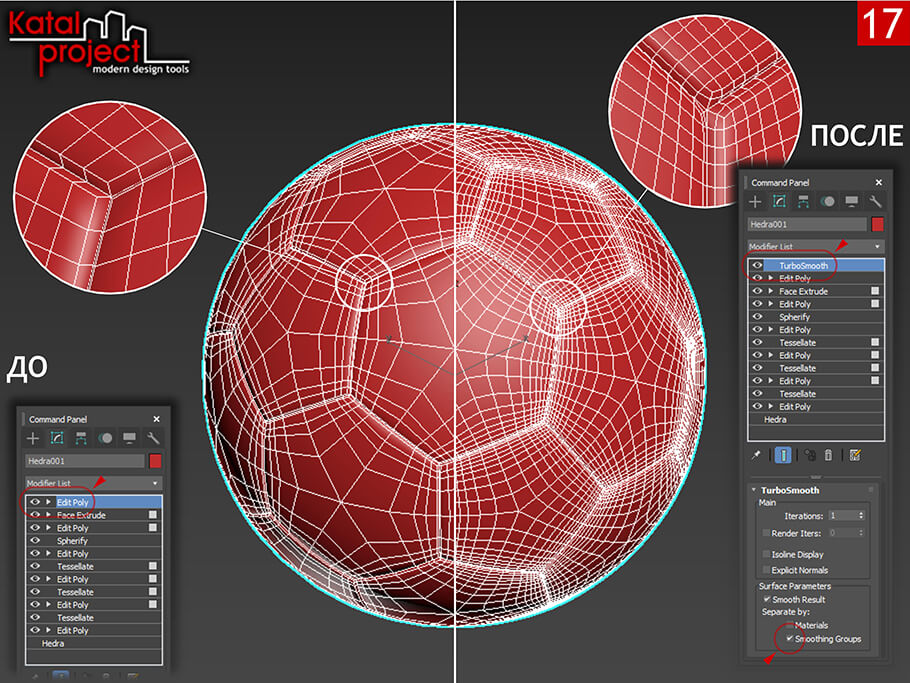
Завершив подготовку можно приступать непосредственно к сглаживанию:

17. Добавляем в стек модификаторов модификатор «TurboSmooth» (Турбо-сглаживание), в параметрах которого, в разделе «Surface Parameters» (Параметры поверхности), включаем галочку «Smoothing Groups» (Группы сглаживания).

Корректировка размера

Несмотря на то, что «отправной точкой» для моделирования мяча был примитив «Hedra» (Многогранник) с радиусом 110,0mm, у готовой модели радиус будет другим. Поэтому, чтобы вернуть футбольному мячу его «законный» радиус, придется выполнить корректировку размеров модели:

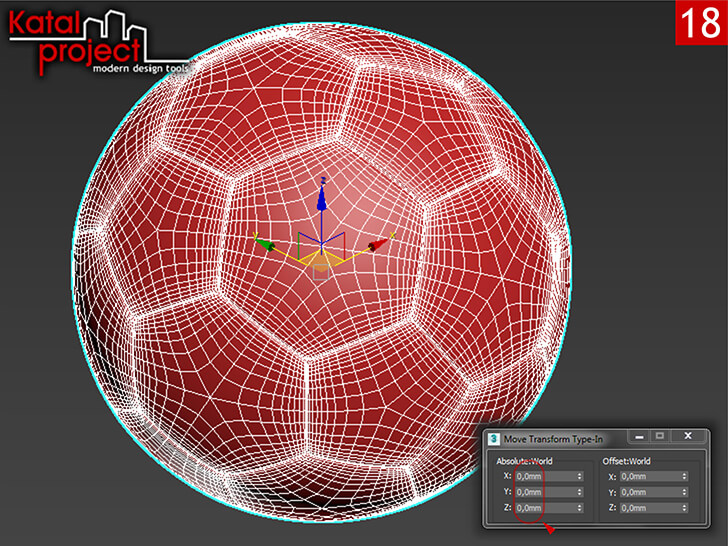
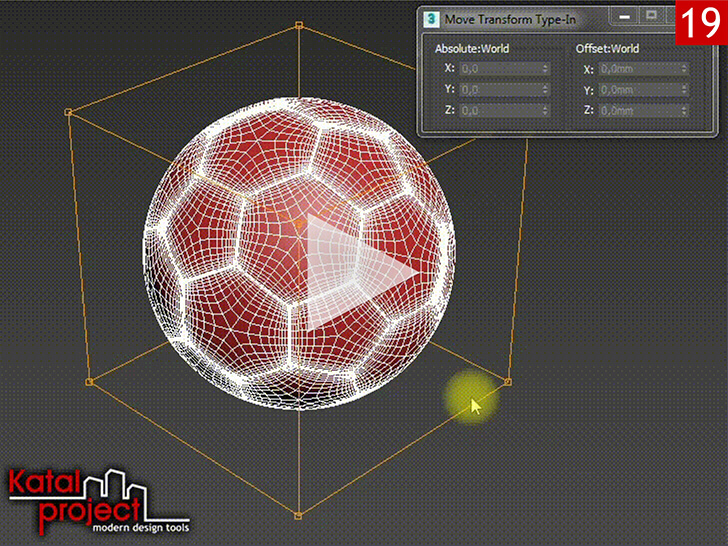
18. Располагаем мяч в начале координат, для чего в диалоговом окне «Move Transform Type-In» (Ввод значений перемещения), в разделе «Absolute: World» (Абсолютные: мировые), вводим следующие координаты:
    • «X» — 0,0mm;
    • «Y» — 0,0mm;
    • «Z» — 0,0mm.
19. Исправляем радиус футбольного мяча:
    • Добавляем в стек модификаторов модификатор «FFD 2x2x2» (Деформация произвольной формы 2x2x2) и активируем уровень «Control Points» (Контрольные точки);
    • Выделяем 4 точки, которые являются вершинами одной из граней кубической решетки, описанной вокруг объекта;
    • В диалоговом окне «Move Transform Type-In» (Ввод значений перемещения), в разделе «Absolute: World» (Абсолютные: мировые) меняем координату, которая отлична от 0,0mm, на 110,0mm (если выделенные точки располагаются с положительной стороны соответствующей координатной оси) или на -110,0mm (если выделенные точки располагаются с отрицательной стороны соответствующей координатной оси);
    • Аналогичным образом располагаем остальные 5 граней решетки, в которую вписан мяч, на расстоянии 110 мм от начала координат;
    • Выходим из режима работы с подчиненными объектами модификатора «FFD 2x2x2» (Деформация произвольной формы 2x2x2).

Видео к уроку

Материалы к уроку

Модель футбольного мяча (файл формата MAX, 736.00 KB): Скачать

Сцена, визуализация которой представлена на обложке урока (файл формата MAX + карты, 27.17 MB): Скачать